My introduction to quantitative portfolio optimization happened during my undergraduate years, inspired by Attilio Meucci’s Risk and Asset Allocation and the convex optimization teachings of Diamond and Boyd at Stanford. With enthusiasm and perhaps more confidence than expertise, I created my first “optimal” portfolio. What struck me most was the disconnect between theory and accessibility. Modern Portfolio Theory had been established since 1990, yet the optimization tools remained largely locked behind proprietary software.
Nevertheless, only a few comprehensive software models are available publicly to use, study, or modify. We tackle this issue by engineering practical tools for asset allocation and implementing them in the Python programming language.
This gap inspired what would eventually be published as: A Python integration of practical asset allocation based on modern portfolio theory and its advancements.
My approach centered on a simple philosophy:
The focus is to keep the tools simple enough for interested practitioners to understand the underlying theory yet provide adequate numerical solutions.
Today, the landscape has evolved dramatically. Projects like PyPortfolioOpt and Riskfolio-Lib have established themselves as sophisticated open-source alternatives, far surpassing my early efforts in both scope and sophistication. Despite its limitations, the project yielded several meaningful insights:
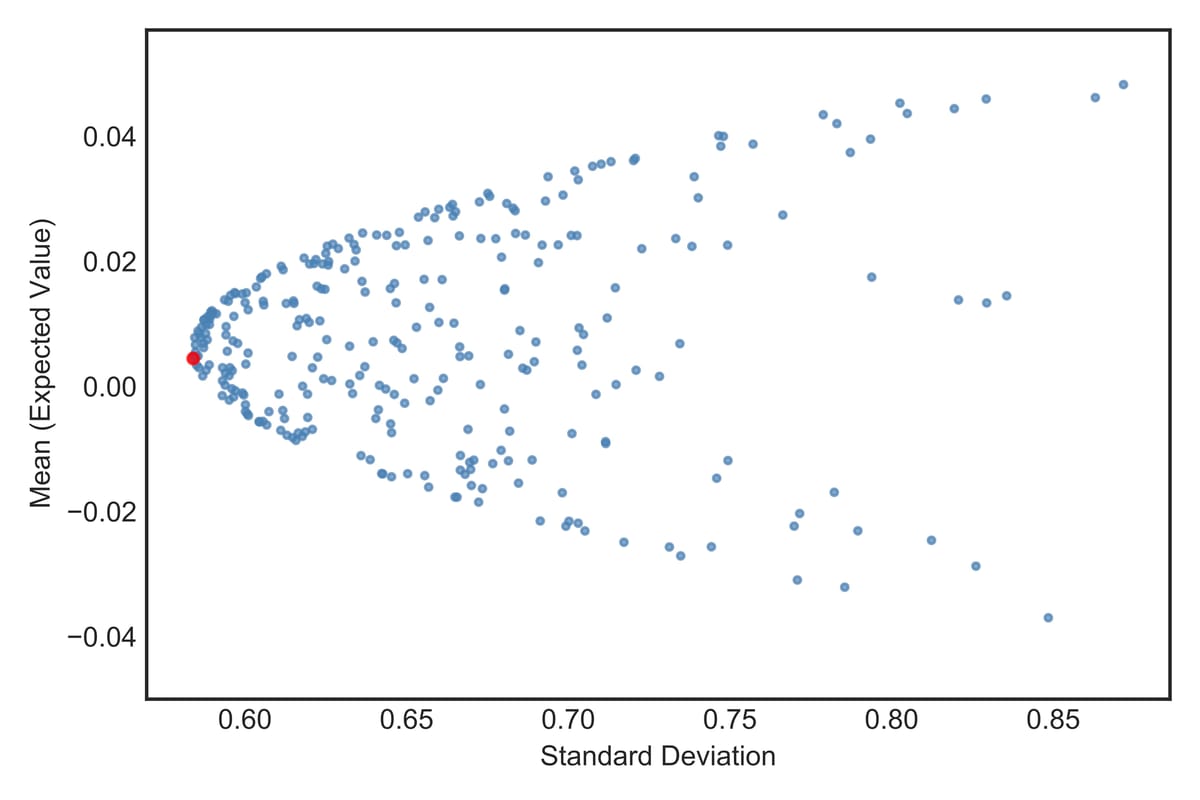
 First, I set out to visualize Modern Portfolio Theory’s fundamental principle—the risk-return tradeoff that drives optimization decisions. This scatter plot showing the efficient frontier demonstrates this core concept.
First, I set out to visualize Modern Portfolio Theory’s fundamental principle—the risk-return tradeoff that drives optimization decisions. This scatter plot showing the efficient frontier demonstrates this core concept.
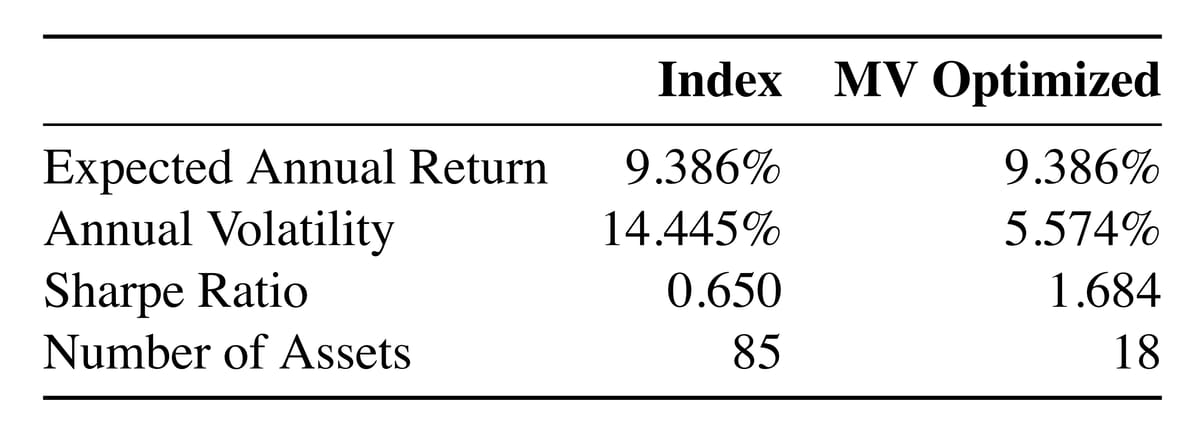
 The results of my first optimization: maintaining a 9.386% return while reducing volatility from 14.445% to 5.574%, effectively tripling the Sharpe ratio from 0.650 to 1.684.
The results of my first optimization: maintaining a 9.386% return while reducing volatility from 14.445% to 5.574%, effectively tripling the Sharpe ratio from 0.650 to 1.684.
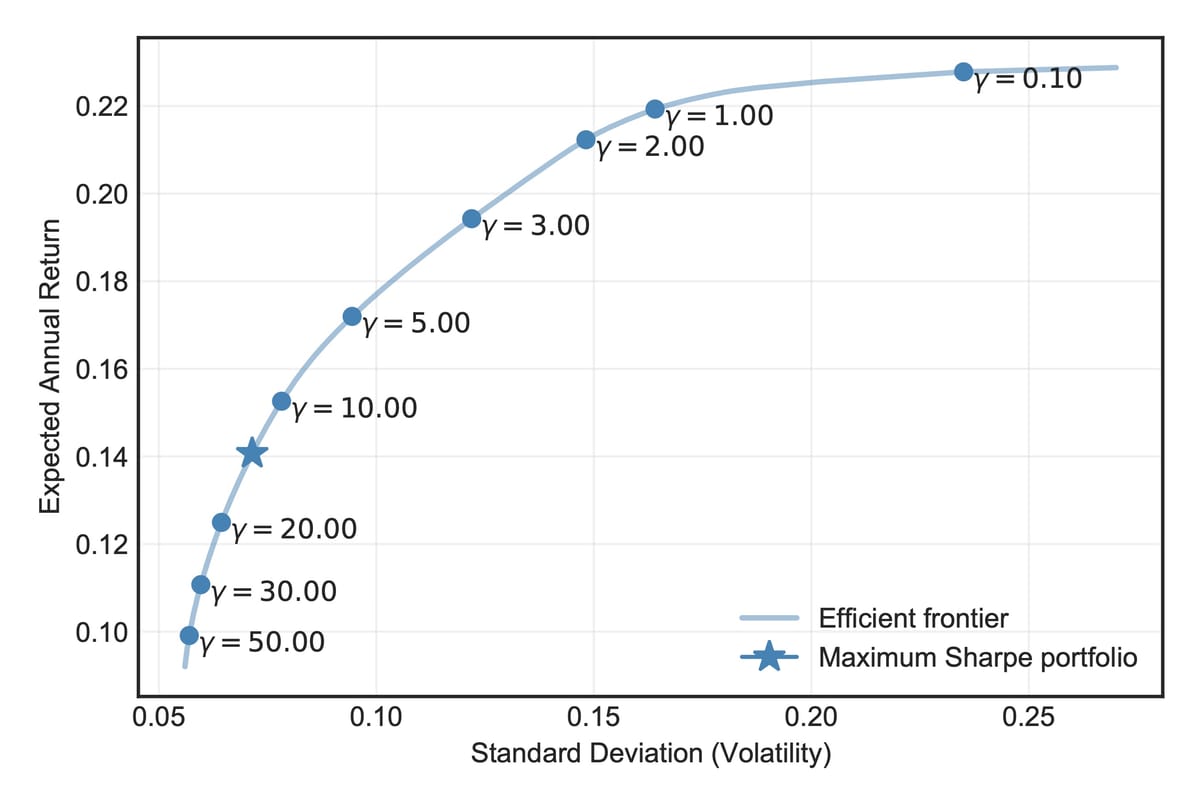
 By varying the risk aversion parameter (gamma), the framework successfully adapted to different investor profiles, showcasing the flexibility of the optimization approach. This efficient frontier plot with different gamma values illustrates how the optimization framework adapts to different investor risk preferences.
By varying the risk aversion parameter (gamma), the framework successfully adapted to different investor profiles, showcasing the flexibility of the optimization approach. This efficient frontier plot with different gamma values illustrates how the optimization framework adapts to different investor risk preferences.
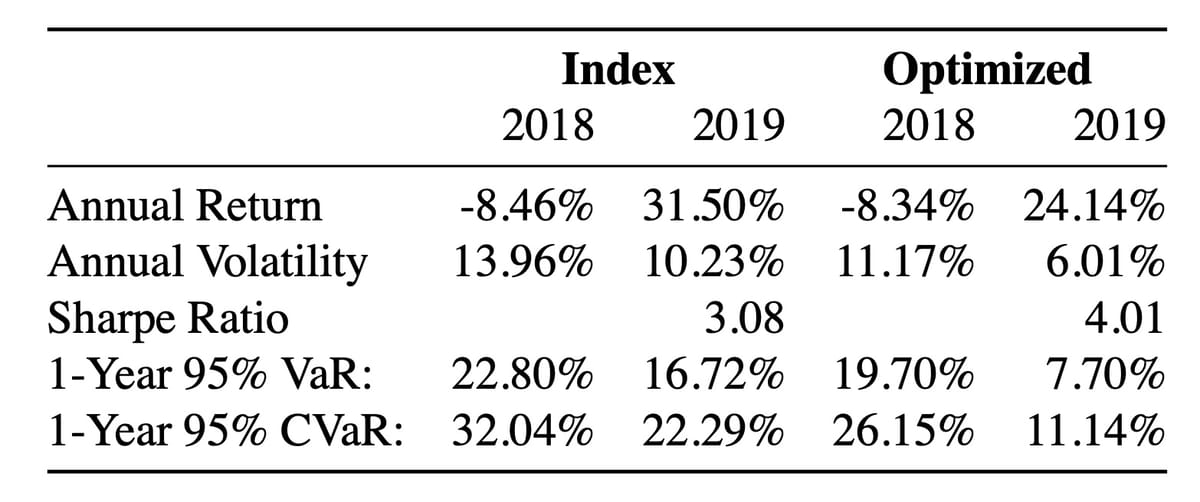
 Perhaps most importantly, out-of-sample testing across diverse market conditions—including the 2018 bear market and 2019 bull market—demonstrated consistent CVaR reduction and improved risk-adjusted returns.
Perhaps most importantly, out-of-sample testing across diverse market conditions—including the 2018 bear market and 2019 bull market—demonstrated consistent CVaR reduction and improved risk-adjusted returns.
We demonstrate how even in an environment with high correlation, achieving a competitive return with a lower expected shortfall and lower excess risk than the given benchmark over multiple periods is possible.
Looking back, the project feels embarrassingly naive—and surprisingly foundational. While it earned some recognition at the time, it now serves as a valuable reminder: sometimes the best foundation is built before you know enough to doubt yourself.